BJT Mismatch parameters

27 September 2021 Link

On This Page



Mismatch parameters

Bipolar mismatch can happen due to 3 parameters:
  1. $I_S$ Mismatch
  2. $β$ Mismatch
  3. $R_E$ Mismatch

There are 2 methods to extract the Bipolar Mismatch parameters. Let us analyze both methods to determine which method represents all 3 mismatch sources adequately.

Measurement Method 1


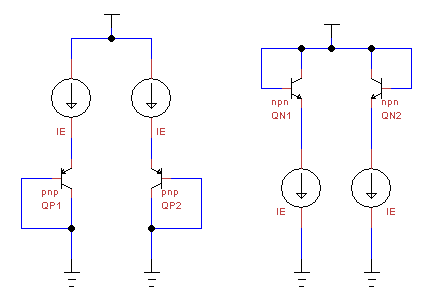
In this method the setup is made as shown above. Here the emitter currents are the same and the difference in the Vbe’s can be directly measured in the 2 side by side devices.
Wehave:
$$ΔV_{BE}=V_{BE1}-V_{BE2}$$


$I_S$ Mismatch only

If the BJT has $I_S$ mismatch only:
$$ΔV_{BE}=V_{BE1}-V_{BE2}=nV_Tln{I_EI_{S2}}/{I_EI_{S1}}=nV_TlnI_{S2}/I_{S1}$$

$$ΔV_{BE}≈nV_T{ΔI_{S}}/I_{S}$$


Beta mismatch Only

If BJT has $β$ mismatch only:
$$ΔV_{BE}=V_{BE1}-V_{BE2}=nV_TlnI_{C1}/I_{C2}$$

$$I_{C1}=β_1/{1+β_1}I_E$$

$$I_{C2}=β_2/{1+β_2}I_E$$

$$ΔV_{BE}=V_{BE1}-V_{BE2}=nV_Tln({β_1(1+β_2)}/{β_2(1+β_1)})$$

Set:
$$β_1=β+{Δβ}/2$$

$$β_2=β-{Δβ}/2$$

$$ΔV_{BE}=nV_Tln({(β+{Δβ}/2)(1+β-{Δβ}/2)}/{(β-{Δβ}/2)(1+β+{Δβ}/2)})$$

$$ΔV_{BE}=nV_Tln(1+{Δβ}/{β(1+β)-{Δβ}/2-({Δβ}/2)^2})$$

$$ΔV_{BE}=nV_T{Δβ}/{β(1+β)}$$


Re Mismatch only

If BJT has $R_E$ mismatch only:
$$ΔV_{BE}=V_{BE1}-V_{BE2}=I_E(R_{E1}-R_{E2})$$


Measurement Method 2


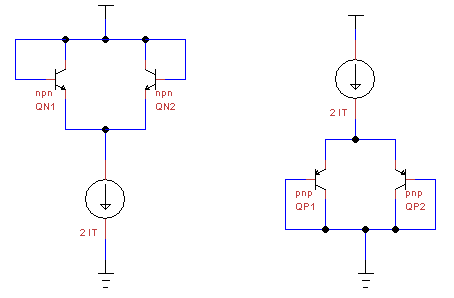
In this method the setup is made as shown above. Here the Vbe’s of both side by side transistors are forced equal and their collector currents can be measured.
$$ΔV_{BE}=V_Tln{I_{C2}}/I_{C1}$$


$I_S$ Mismatch only

$$I_{C1}=I_{S1}exp(V_{BE}/{nV_T})$$
$$I_{C2}=I_{S2}exp(V_{BE}/{nV_T})$$

$$I_{C2}/I_{C1} = I_{S2}/I_{S1}$$

$$ΔV_{BE}=V_Tln{I_{S2}}/I_{S1}$$


Beta mismatch Only

Since $I_S$ will be same and $V_{BE}$ is the same the measured $I_C$ will be the same so we do not detect any mismatch due to Beta mismatch.

Re Mismatch only

$$ΔV_{BE}=V_Tln{I_{C2}}/I_{C1}$$
$$I_{C1}=αI_{E1}$$

$$I_{C2}=αI_{E2}$$

$$I_{C2}/I_{C1}=I_{E2}/I_{E1}$$

$$ΔV_{BE}=V_Tln{I_{E2}}/I_{E1}$$

$$I_{E1}R_{E1}+V_{BE1}=I_{E2}R_{E2}+V_{BE2}$$

$$I_{E1}=I_T+{ΔI}/2$$

$$I_{E2}=I_T-{ΔI}/2$$

$$R_{E1}=R_E+{ΔR_E}/2$$

$$R_{E2}=R_E-{ΔR_E}/2$$

$$I_{E1}R_{E1}-I_{E2}R_{E2}=I_TΔR_E+R_EΔI$$

$$⇒I_TΔR_E+R_EΔI=nV_Tln{I_{E2}}/I_{E1}$$

$$⇒I_TΔR_E+R_EΔI=nV_Tln(1-{ΔI}/I_{E1})$$

$$⇒I_TΔR_E+R_EΔI≈-nV_T{ΔI}/I_{E1}=-nV_T{I_{E1}-I_{E2}}/I_{E1}=-nV_T(1-I_{E2}/I_{E1})$$

Setting $ΔI=I_{E1}{I_{E1}-I_{E2}}/I_{E1}≈I_{T}(1-I_{E2}/I_{E1})$
$$⇒I_TΔR_E+R_EI_{T}(1-I_{E2}/I_{E1})=-nV_T(1-I_{E2}/I_{E1})$$

Solving for $I_{E2}/I_{E1}$:
$$I_{E2}/I_{E1}=1+{I_TΔR_E}/{nV_T+I_TR_E}$$

$$∴ΔV_{BE}=V_TlnI_{E2}/I_{E1}=V_Tln(1+{I_TΔR_E}/{nV_T+I_TR_E})≈V_T{I_TΔR_E}/{nV_T+I_TR_E}$$


Comparison of the Methods

Mismatch Factor Method 1 Method 2Comment
$I_S$$ΔV_{BE}=nV_TlnI_{S2}/I_{S1}$$ΔV_{BE}=V_Tln{I_{S2}}/I_{S1}$Both methods represent this mismatch
$β$$$ΔV_{BE}=nV_T{Δβ}/{β(1+β)}$$$ΔV_{BE}=0$Method 2 cannot measure the mismatch due to Beta
$R_E$$ΔV_{BE}=I_E(R_{E1}-R_{E2})$$ΔV_{BE}≈V_T{I_TΔR_E}/{nV_T+I_TR_E}$Method 1 gives a better reading

This Method 1 should be the method used to measire the mismatch parameter for a BJT since it includes effects from all 3 mismatch parameters.
NOTE: Mismatch will increase with temperature due to $V_T$ dependance