Brokaw Bandgap Gm Analysis

20 August 2019 Link

On This Page



Cell 1

The basic cell has a structure as shown below: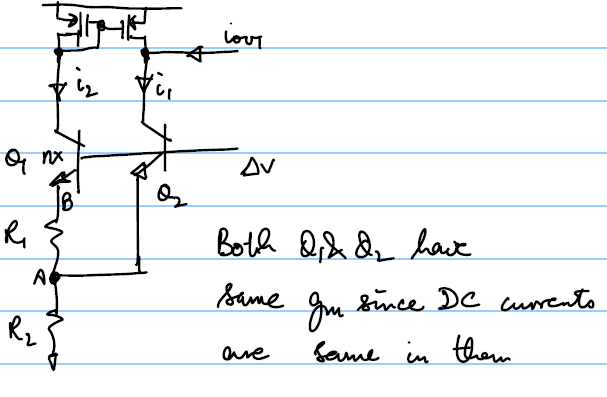


Analysis

We have:
$$i_{out}=i_1-i_2$$

$$i_1=g_m(Δv-v_A)$$

$$i_2=g_m(Δv-v_B)$$

Putting these in the 1st equation we have:
$$i_{out}=g_m(v_B-v_A)....(1)$$

Also $[g_m(Δv-v_B)+g_m(Δv-v_A)]R_2=v_A$. From this we can solve for $v_A$ and we have:
$$v_A=(2Δv-v_B){g_mR_2}/{1+g_mR_2}...(2)$$

Also $v_B-v_A=g_m(Δv-v_B)R_1$. From this and using the $v_A$ value from (2) we have:
$$v_B=Δv{g_mR_1+{2g_mR_2}/{1+g_mR_2}}/{1+g_mR_1+{g_mR_2}/{1+g_mR_2}}...(3)$$

Substituting $v_B$ from (3) and $v_A$ from (2) into (1) we have:
$$i_{out}=g_m[Δv{g_mR_1+{2g_mR_2}/{1+g_mR_2}}/{1+g_mR_1+{g_mR_2}/{1+g_mR_2}}(1+{g_mR_2}/{1+g_mR_2})-{2Δvg_mR_2}/{1+g_mR_2}]$$

Dividing by $Δv$ and simplifying we have:
$$G_M=i_{out}/{Δv}=1/{1/{g_m^2R_1}+1/g_m(1+2R_2/R_1)+R_2}$$

$$G_M={g_m^2R_1}/{1+g_mR_1+2g_mR_2+g_m^2R_1R_2}$$

By substituting $g_m={\ln n}/R_1$ and taking approximations we have:
$$G_M≈1/{1/g_m(1+2R_2/R_1)+R_2}=1/{R_1/{\ln n}(1+2R_2/R_1)+R_2}≈1/{2R_2/{\ln n}+R_2}=1/R_2[{\ln n}/{2+\ln n}]$$


Useful numbers

Normally the n factor is set to 8 since that allows good layout. With n = 8 we have
$$G_M=0.51/R_2≈1/{2R_2}$$

Even if n=4 we have $G_M=0.4/R_2$ which is still close with about 25% error. So the number $1/{2R_2}$ is good to keep handy

Cell 2

This alternate topology has a structure as shown below: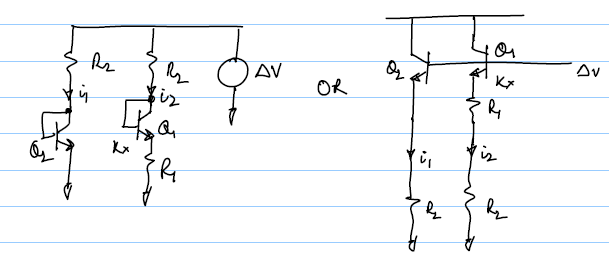


Analysis

Both topologies follow the same analysis:
$$i_{out}=i_1-i_2$$

$$i_1=g_m(Δv-i_1R_2)={g_mΔv}/{1+g_mR_2}$$

$$i_2=g_m(Δv-i_2(R_1+R_2))={g_mΔv}/{1+g_m(R_1+R_2)}$$

Therefore we have:
$$i_{out}={g_mΔv}/{1+g_mR_2}-{g_mΔv}/{1+g_m(R_1+R_2)}$$

$$⇒i_{out}/{Δv}=G_M={g_m^2R_1}/{(1+g_m(R_1+R_2))(1+g_mR_2)}$$

If $g_mR_2≫1$ then we can approximate $G_M$ as:
$$G_M≈R_1/{R_2(R_1+R_2)}$$


Useful Numbers

Remember that the bandgap voltage is about 1.2V and Vbe is about 0.6V so in this case we have:
$${V_T\ln n}/R_1R_2≈0.6V$$

So for n=8 we have $R_2=11.1R_1$, putting this in the $G_M$ equation we have
$$G_M≈1/{12.1R_2}$$


Comparing the Transconductances

$$({g_m^2R_1}/{1+g_mR_1+2g_mR_2+g_m^2R_1R_2})_I◌({g_m^2R_1}/{1+g_mR_1+2g_mR_2+g_m^2R_1R_2+g_m^2R_2^2})_{II}$$

It is clearly seen than the $G_{M-I}>G_{M-II}$ because of the extra term $g_m^2R_2^2$ in the denominator. Hence the topology 1 always provides better accuracy by making the effects of mismatch and offset for the same bias currents lower.

From the numbers we also see that for n=8 the 1st topology provides 6 times more $G_M$.


References

| | | |