In this article I derive the transfer function for the Buck converter switching transfer function. This transfer function can then be used in calculating the loop gain of a Buck Regulator or its output impedance.

The Circuit

[top]

The circuit I will use for the derivation is here: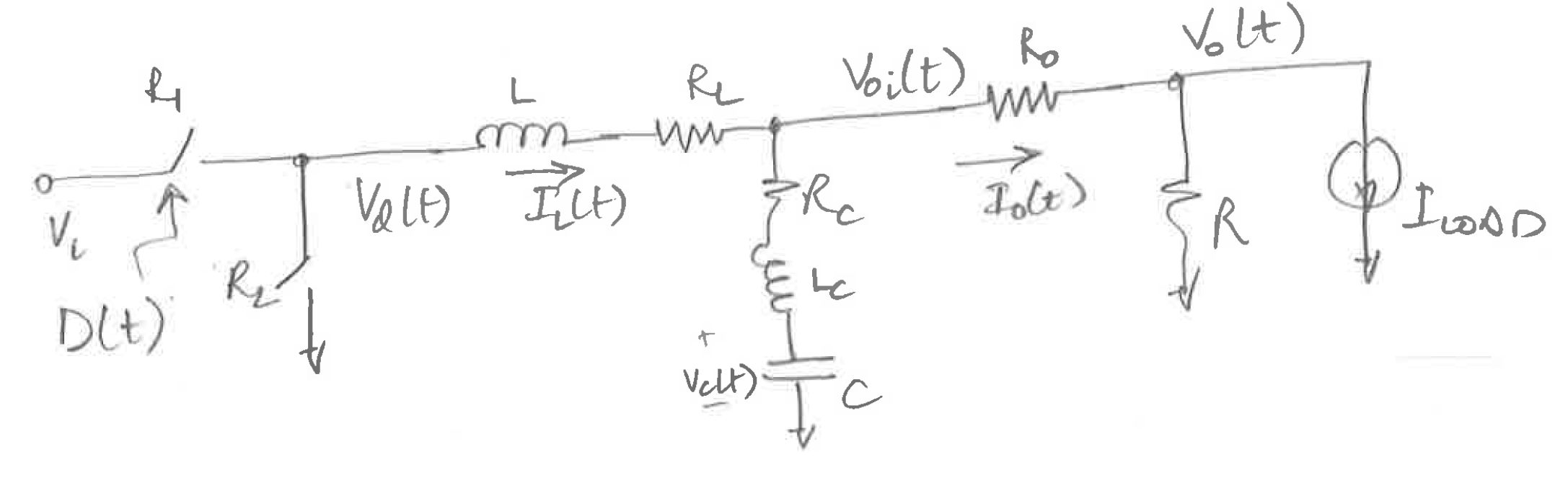

In the above circuit I have included the parasitic elements as well. This includes parasitic resistance in the inductance and the output capacitance as well as the parasitic inductance of the output capacitance and the parasitic resistance of the output wiring to the load.

The derivation

[top]

The derivation is not difficult to follow just tedious to do. We start by defining $V_d(t)$ based on D(t)
$V_d(t)=V_i-I_L(t) R_1$ when $D(t)=1$
$V_d(t)=-I_L(t) R_2$ when $D(t)=0$
Combining these 2 we can write:

also writing the loop equation across the inductor branch we have:

The equation for the cap can be written as:

Writing the branch equation across the parasitic components of the cap we have:

Substituting (3) in the above equation we get:

Now write the loop equation across the parasitic output resistance:

Now we have equations (1) - (5). We can eliminate $V_d(t),V_C(t),V_{oi}(t),I_L(t)$ to get ${V_O(t)}/{D(t)}$
Put (5) in (2) to get:

Put (5) in (4) to get:

Now we can eliminate $V_d(t) $ (1) and (6) to get:

Now we just have 3 equations (3), (7) and (8) and we need to eliminate $V_C(t)$ and $I_L(t)$.

Linearizing the equations

[top]

To eliminate them we would have to solve differential equations but that is not needed since we need to analyze the small signal behaviour at the steady state. So let us get the small signal equivalent equations for (3), (7) and (8).
Here D(t) is a discrete value of 0 or 1, converting that to small signal would not make any sense but if we look at the averages and look at the small signal of the averages then it would make sense.
The equations (3), (7) and (8) would work for the averages as well.
The small signal conversions we can use are:

Equation(3) becomes:

or

Equation (7) becomes:

Equation (8) becomes:


Now we can take the Laplace transform of the equations (a),(b) and (c):
Equation (a) becomes:

Equaion (b) becomes:

Equation (c) becomes:


From (ii) we get:

Put this in (i):

Put these in (iii) we get:


This expression contains all parasitic components as well. We can check whether it matches the ideal expression when making the parasitics 0 and switches ideal:


which can also we written as:


This is the ideal buck converter switching transfer function.

In the next follow up article I will show how we can verify this with simulation.

See Also

[top]

• Boost Converter Switching transfer function for stability Analysis
• Hysteresitc Buck feedback networks