DNL

[top]

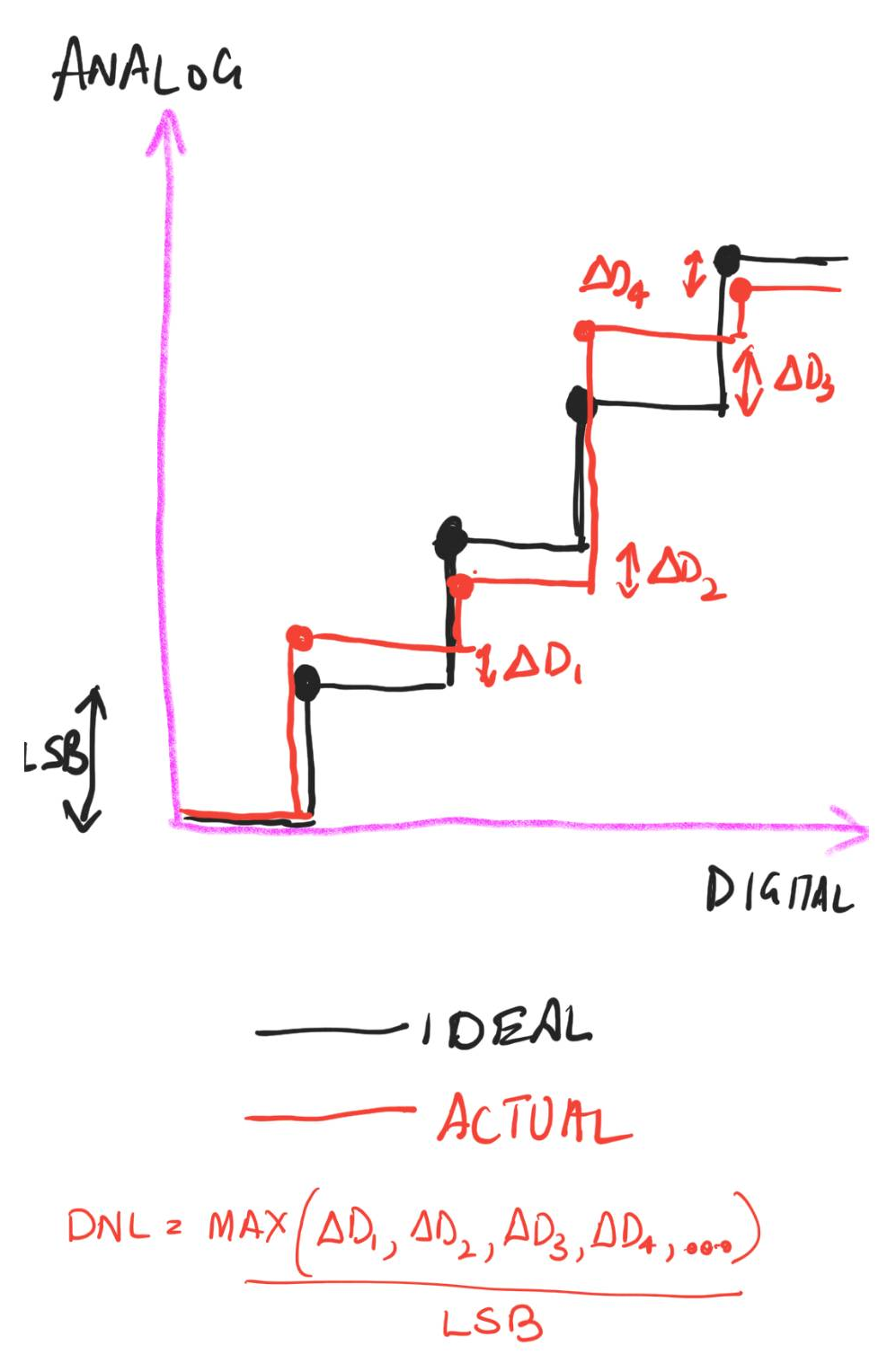
DNL is an abbreviation for Differential Non Linearity. It is a measure of the maximum deviation over the whole range of the step in the Analog input/output from an ideal 1 LSB step. This report shows some good graphs to understand DNL.
As an example if supplose a DAC has a LSB step of 1mV so that means that every next input code the output voltage should increase by exactly 1mV. But depending on the circuit non linearities/mismatches and operating point the steps may be like 0.991mV, 1.001mV, 0.99mV.... So DNL is given by:

This is shown int he diagram below:

Cadence

[top]

The DNL for a DAC which can be simulated through its range using a DC sweep simulation and using a simple formula in Cadence Calculator. Here is the procedure to do that:

1. Create a test bench with the DAC with all sources with DC values so that the DC simulation can power up.
2. The input to the DAC can be given by a ADC created using verilog AMS. The following code can be used to create a ADC that can simulate in a DC simulation:

   `include "discipline.h"
   `include "constants.h"
    
   module adc_8bit_dc(vd7, vd6, vd5, vd4, vd3, vd2, vd1, vd0, vin);
   electrical vd7, vd6, vd5, vd4, vd3, vd2, vd1, vd0, vin;
   parameter real vlogic_high = 5;
   parameter real vlogic_low  = 0;
   parameter real vref        = 1.0;
    
   `define NUM_ADC_BITS    8
      real unconverted;
      real halfref;
    
      real vd[0:`NUM_ADC_BITS-1];
      integer i;
    
      analog begin
    
         halfref = vref / 2;
            unconverted = V(vin);
            for (i = (`NUM_ADC_BITS-1); i >= 0 ; i = i - 1) begin
               vd[i] = 0;
               if (unconverted > halfref) begin
                  vd[i] = vlogic_high; 
                  unconverted = unconverted - halfref;
           end else begin
                  vd[i] = vlogic_low;
           end
               unconverted = unconverted * 2;
            end
    
    
         //
         // assign the outputs
         //
           V(vd7) <+ vd[7];
             V(vd6) <+ vd[6];
         V(vd5) <+ vd[5];
         V(vd4) <+ vd[4];
         V(vd3) <+ vd[3];
         V(vd2) <+ vd[2];
         V(vd1) <+ vd[1];
         V(vd0) <+ vd[0];
    
   `undef NUM_ADC_BITS
      end
   endmodule
   

3. Now connect the output digital bus of this ADC symbol to the DAC input.
4. The input of the ADC is connected to a voltage source whose DC voltage is set to a variable like "vin"
5. The parameters of the ADC should be set as follows:
   1. vlogic_high - Set to the logic high level of the bus
   2. vlogic_low - Set to the logic low level of the bus
   3. vref - This is the most important parameter for correct simulation. Calculate it as follows. If the LSB for this ADC you want to set as L then the vref = L*2^(NUM_ADC_BITS). So for example for an LSB of 5mV for an 8 bit ADC the vref should be set to 1.28V
6. Now run a DC sweep simulation where you sweep the "vin" variable from a value less than L with a step of L all the way to vref
7. Since we step with L every DC sweep evaluation point will generate a new code and hence a new output from the DAC. So the DAC output will look like a perfectly straight line with a a constant slope.
8. Now use this formula to calculate the +ve and -ve DNL and the absolute

   $DNL_+$=ymax(deriv(VS("/OUT"))*VAR("vinstep")/VAR("LSB")-1)$$}}}

   $DNL_-$=ymin(deriv(VS("/OUT"))*VAR("vinstep")/VAR("LSB")-1)

   DNL=ymax(abs(deriv(VS("/OUT"))*VAR("vinstep")/VAR("LSB")-1))

   Here LSB is the output voltage LSB value.

   vinstep is L described above

   You may have to clip VS("/OUT") if the sweep in vin exceeds the DAC input range and you may have to clip deriv(VS("/OUT")) to remove the 1st point. It can be clipped from offset+vinstep to (2^bits-1)*vinstep+offset. Where offset it the sweep starting value (less than L)

NOTE
For a DAC if the output at 0 code (all 0) is 0 then LSB = Vo/(2^bits-1) where Vo is the full scale output (at all 1s)
For a DAC if the output at 0 code (all 0) is 1 Vi then LSB = (Vo-Vi)/(2^bits-1). If Vi = 1 LSB then this is equivalent to LSB = Vo/(2^bits)

References

[top]

• Calculating INL in Cadence
• TI Note on Understanding Data Converters