A basic differential amplifier input stage looks like:
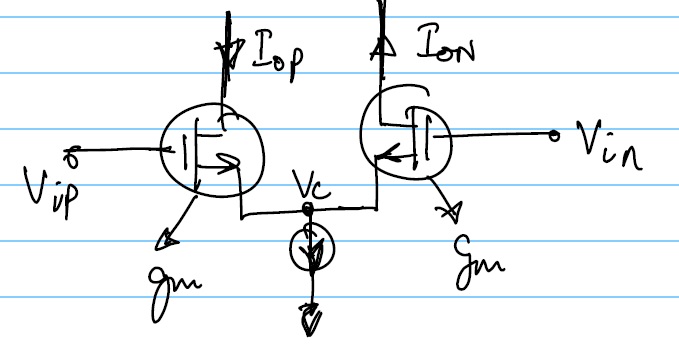
Vip, Vin, Iop and Ion are small signal quantities
NOTE: $I_{op}=I_{on}$
$G_m = I_{out}/V_{in}$ $V_{in}$ is always defined as $=V_{ip}-V_{in}$
Now we need to define what is $I_{out}$
CASE 1: Output is differntial so the output current $I_{out}=I_{op}=I_{on}$
This is because to produce a differential output over symmetric resistances:
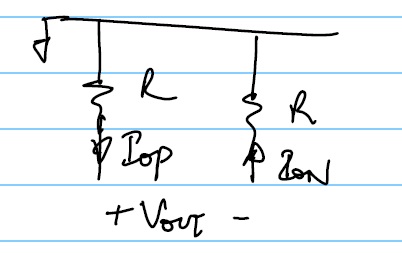
$$V_{out} = -I_{op}R-I_{on}R = -2I_{out}R$$
Thus we get the differential voltage properly
$$ ∴ G_m=I_{op}/{V_{ip}-V_{in}} = I_{op}/{(V_{ip}-V_c)-(V_{in}-V_c)}$$
$$ ⇒ G_m=I_{op}/{I_{op}/g_m-(-I_{on}/g_m)} = I_{op}/{ {I_{op}+I_{op}} /g_m} = g_m/2$$
CASE 2: Output is single ended by active mirroring as shown below:
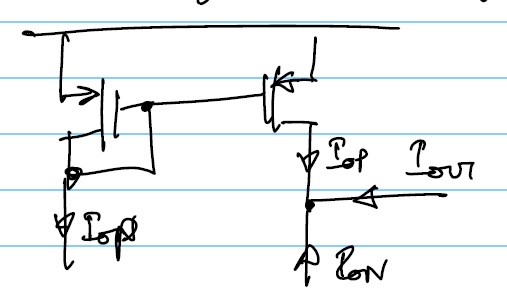
$$I_{out}=-(I_{op}+I_{on}) = -2I_{op}$$
$$ ∴ G_m=2 I_{op}/{I_{op}/g_m-(-I_{on}/g_m)} = -2I_{op}/{2I_{op}} g_m = -g_m$$
For Example:
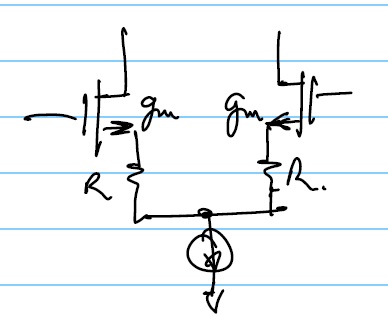
CASE 1: $$G_m=g_m/{2(1+g_mR)}$$
CASE 2: $$G_m=g_m/{1+g_mR}$$
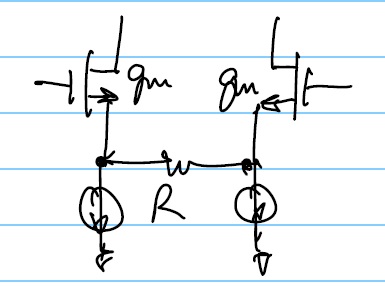
CASE 1: $$G_m=g_m/{2(1+g_mR/2)}$$
CASE 2: $$G_m=g_m/{1+g_mR/2}$$

Vip, Vin, Iop and Ion are small signal quantities
NOTE: $I_{op}=I_{on}$
$G_m = I_{out}/V_{in}$ $V_{in}$ is always defined as $=V_{ip}-V_{in}$
Now we need to define what is $I_{out}$
CASE 1: Output is differntial so the output current $I_{out}=I_{op}=I_{on}$
This is because to produce a differential output over symmetric resistances:

$$V_{out} = -I_{op}R-I_{on}R = -2I_{out}R$$
Thus we get the differential voltage properly
$$ ∴ G_m=I_{op}/{V_{ip}-V_{in}} = I_{op}/{(V_{ip}-V_c)-(V_{in}-V_c)}$$
$$ ⇒ G_m=I_{op}/{I_{op}/g_m-(-I_{on}/g_m)} = I_{op}/{ {I_{op}+I_{op}} /g_m} = g_m/2$$
CASE 2: Output is single ended by active mirroring as shown below:

$$I_{out}=-(I_{op}+I_{on}) = -2I_{op}$$
$$ ∴ G_m=2 I_{op}/{I_{op}/g_m-(-I_{on}/g_m)} = -2I_{op}/{2I_{op}} g_m = -g_m$$
- Thus the OTA which produces single ended outputs by active mirroring have $G_m = g_m$
- The OTA which produces differential output or just takes the current from 1 branch of the diffamp have $G_m=g_m/2$
For Example:

CASE 1: $$G_m=g_m/{2(1+g_mR)}$$
CASE 2: $$G_m=g_m/{1+g_mR}$$

CASE 1: $$G_m=g_m/{2(1+g_mR/2)}$$
CASE 2: $$G_m=g_m/{1+g_mR/2}$$