Lead Lag Network

20 August 2019 Link

On This Page



The network

The following circuit shows the lead-lag network which creates 2 poles and 2 zeroes: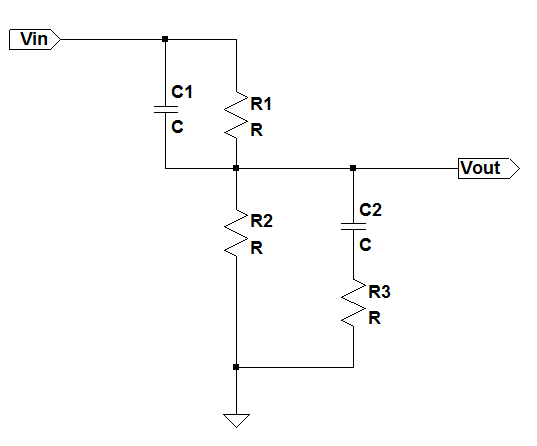


Solution

The $V_{in}$ to $V_{out}$ transfer function can be written as:

$$V_{out}/V_{in} = { {(R_3+1/{sC_2})R_2}/{R_3+1/{sC_2}+R_2} }/{ {(R_3+1/{sC_2})R_2}/{R_3+1/{sC_2}+R_2}+R_1/{sR_1C_1+1} } $$

This can be simplified to:
$$V_{out}/V_{in} = { (sR_3C_2+1)R_2(sR_1C_1+1) }/{(sR_3C_2+1)R_2(sR_1C_1+1)+R_1(sC_2(R_2+R_3)+1)}$$


Zeroes and Poles

So we see the 2 zeros created are:
$$z_1=-1/{R_3C_2}$$

$$z_2=-1/{R_1C_1}$$

The 2 poles can be calculated if we solve the denominator which can we written as:
$$s^2R_1R_2R_3C_1C_2+s(R_1R_2C_1+R_2R_3C_2+R_1C_2(R_2+R_3))+R_1+R_2=0$$

or
$$s^2R_3C_1C_2R_1||R_2+s(R_1||R_2(C_1+C_2)+R_3C_2)+1=0$$

If we substitute the following:
$$A=R_3C_1C_2R_1||R_2$$

$$B=R_1||R_2(C_1+C_2)+R_3C_2$$

we can write (3) as:
$$As^2+Bs+1=0$$

We can solve for s as:
$$s={-B±√{B^2-4A} }/{2A}$$

$$s=-B/{2A}±B/{2A}√{1-{4A}/B^2}$$

Now to simplify further we need to see the relative magnitudes to decide what terms can be neglected. Comparing A and B we can clearly see that if the circuit time constants are lower than even a milli second A ≪ B. That is because A is a product of 2 time constants while B is a time constant. Usually the network is designed to have 1 time constant much smaller than the other. So consider the case when one time constant is 100 times larger than the other. For example $R_3C_2 ≫ R_1||R_2C_1$. This means that the magnitude of $A/B^2$ = 100/10000 or $4A/B^2=4/100$. So $B^2$ is still 25 times larger than 4A.

So from this point on the assumption and approximation that we take is:

One time constant in the circuit is more dominant than the other one.

So now we can approximate the poles now as:
$$s≈-B/{2A}±B/{2A}(1-{2A}/B^2)$$

$$p_1≈-1/B ; p_2≈-B/A$$

So substituting the values of A and B in we get the final poles of the circuit as:
$$p_1≈-1/{R_1||R_2(C_1+C_2)+R_3C_2}$$

$$p_2≈-{R_1||R_2(C_1+C_2)+R_3C_2}/{R_3C_1C_2R_1||R_2}$$


If $C_1≪C_2$ and $R_3≪R_1||R_2$ then we can approximate the poles as:
$$p_1≈-1/{R_1||R_2C_2}$$

$$p_2≈-1/{R_3C_1}$$


See Also

  1. Compensation Techniques
  2. The book Frequency Compensation Techniques for Low-Power Operational Amplifiers (The Springer International Series in Engineering and Computer Science) has good chapter on compensation analysis of multi stage opamps.
  3. The book Op Amps for Everyone, Fourth Edition has a good chapter on different networks for compensating opamps