Circuit Diagram

[top]

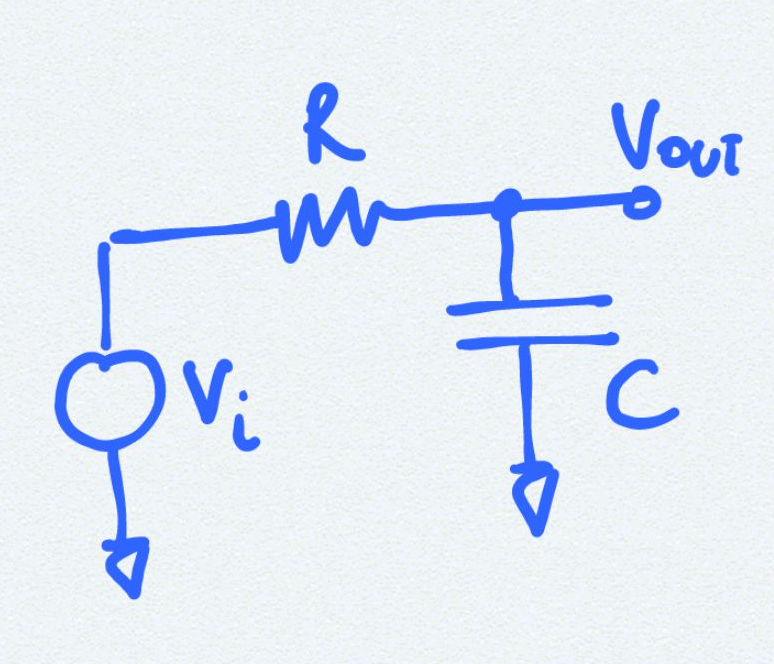
Analysis

[top]

Although this is a very simple and well known circuit some interesting questions here and results here that we derive here is

• What happens when $V_i$ is a ramp rather than a step.
• How does the output voltage behave different ramp slopes

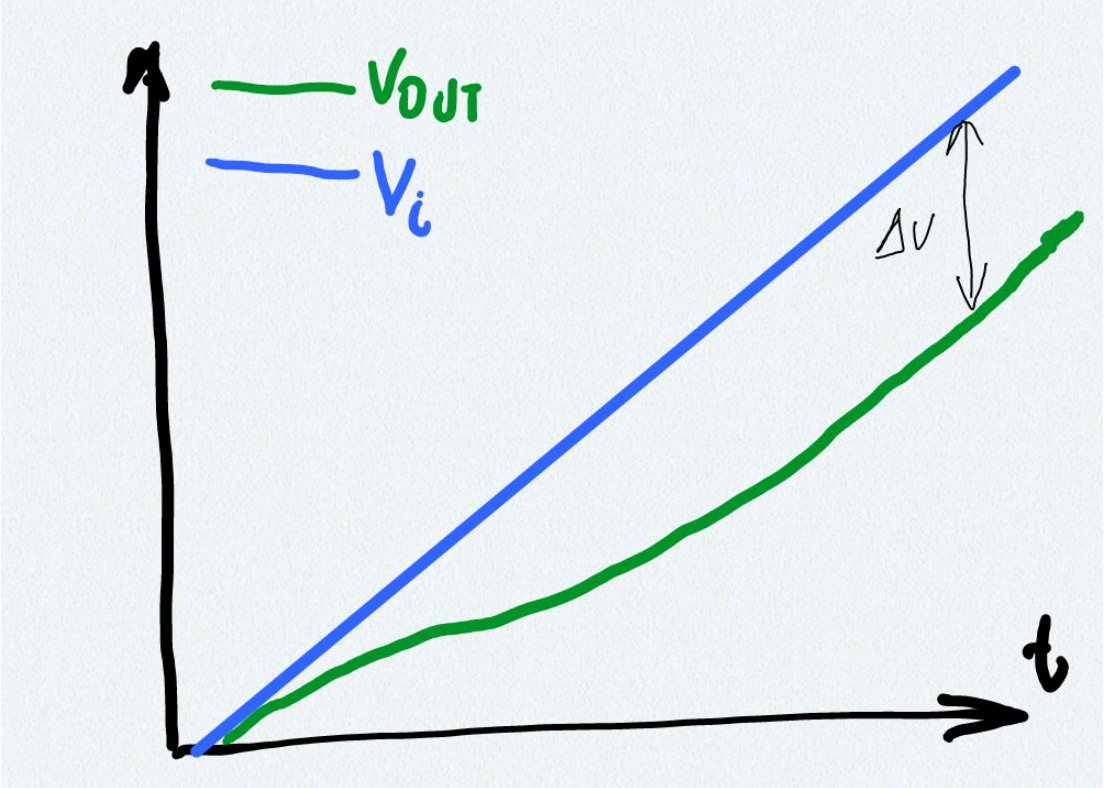
Why are those important? If we know how soon the output catches up to a ramp and what is the voltage lag we can determine the RC values that give the desired response to a ramp input encountered so often in circuits.

Let $V_i=Mt$ where M is the ramp slope and t is time so we have:



Solving this differential equation for $V_{out}$ by multiplying with $e^{t/{RC}}$ and integrating we get:

where $A_o$ is the integration constant which can be solved by the initial condition at t=0 $V_{out}=0$
Thus $A_o=MRC$
So we have:


So now lets look at $V_{out}$ after certain number of time constants say K i.e. $t=KRC$ so we have:

Here we can write $V_i=MKRC$ therefore we have:


Therefore the output would start tracking after a couple of time constants and the difference (voltage lag) between the output and the input is approximately MRC.

Amplitude limited ramp

[top]

An amplitude limited ramp is given as


To make a good ramp follower RC circuit the time $t_F≫RC$ so that it starts following the ramp much before the ramp reaches its limit

References

[top]

| | | |
| | | |